Pot Odds Poker Explained
As daunting as it sounds, it is simply a tool that we use during the decision making process to calculate the Pot Odds in Poker and the chances of us winning the pot. Remember, Poker is not based on pure luck, it is a game of probabilities, there are a certain number of cards in the deck and a certain probability that outcomes will occur. Pot odds are defined as the ratio between the size of the pot and the bet facing you. For example, if there is $4 in the pot and your opponent bets $1, you are being asked to pay one-fifth of the pot in order to have a chance of winning it. A call of $1 to win $5 represents pot odds of 5:1.
This is a very important lesson and can also be quite intimidating to a lot of people as we are going to discuss Poker Math!
But there is no need for you to be intimidated, Poker Maths is very simple and we will show you a very simple method in this lesson.
You won’t need to carry a calculator around with you or perform any complex mathematical calculations.
What is Poker Math?
As daunting as it sounds, it is simply a tool that we use during the decision making process to calculate the Pot Odds in Poker and the chances of us winning the pot.
Remember, Poker is not based on pure luck, it is a game of probabilities, there are a certain number of cards in the deck and a certain probability that outcomes will occur. So we can use this in our decision making process.
Every time we make a decision in Poker it is a mathematical gamble, what we have to make sure is that we only take the gamble when the odds are on in our favour. As long as we do this, in the long term we will always come out on top.
When to Use Poker Maths
Poker Maths is mainly used when we need to hit a card in order to make our hand into a winning hand, and we have to decide whether it is worth carrying on and chasing that card.
To make this decision we consider two elements:
- How many “Outs” we have (Cards that will make us a winning hand) and how likely it is that an Out will be dealt.
- What are our “Pot Odds” – How much money will we win in return for us taking the gamble that our Out will be dealt
We then compare the likelihood of us hitting one of our Outs against the Pot Odds we are getting for our bet and see if mathematically it is a good bet.
The best way to understand and explain this is by using a hand walk through, looking at each element individually first, then we’ll bring it all together in order to make a decision on whether we should call the bet.
Consider the following situation where you hold A 8 in the big blind. Before the flop everyone folds round to the small blind who calls the extra 5c, to make the Total pot before the Flop 20c (2 players x 10c). The flop comes down K 9 4 and your opponent bets 10c. Let’s use Poker Math to make the decision on whether to call or not.
Poker Outs
When we are counting the number of “Outs” we have, we are looking at how many cards still remain in the deck that could come on the turn or river which we think will make our hand into the winning hand.

In our example hand you have a flush draw needing only one more Club to make the Nut Flush (highest possible). You also hold an overcard, meaning that if you pair your Ace then you would beat anyone who has already hit a single pair on the flop.
From the looks of that flop we can confidently assume that if you complete your Flush or Pair your Ace then you will hold the leading hand. So how many cards are left in the deck that can turn our hand into the leading hand?
- Flush – There are a total of 13 clubs in the deck, of which we can see 4 clubs already (2 in our hand and 2 on the flop) that means there are a further 9 club cards that we cannot see, so we have 9 Outs here.
- Ace Pair – There are 4 Ace’s in the deck of which we are holding one in our hand, so that leaves a further 3 Aces that we haven’t seen yet, so this creates a further 3 Outs.
So we have 9 outs that will give us a flush and a further 3 outs that will give us Top Pair, so we have a total of 12 outs that we think will give us the winning hand.
So what is the likelihood of one of those 12 outs coming on the Turn or River?
Professor’s Rule of 4 and 2
An easy and quick way to calculate this is by using the Professor’s rule of 4 and 2. This way we can forget about complex calculations and quickly calculate the probability of hitting one of our outs.
The Professor’s Rule of 4 and 2
- After the Flop (2 cards still to come… Turn + River)
Probability we will hit our Outs = Number of Outs x 4 - After the Turn (1 card to come.. River)
Probability we will hit our Outs – Number of Outs x 2
So after the flop we have 12 outs which using the Rule of 4 and 2 we can calculate very quickly that the probability of hitting one of our outs is 12 x 4 = 48%. The exact % actually works out to 46.7%, but the rule of 4 and 2 gives us a close enough answer for the purposes we need it for.
If we don’t hit one of our Outs on the Turn then with only the River left to come the probability that we will hit one of our 12 Outs drops to 12 x 2 = 24% (again the exact % works out at 27.3%)
To compare this to the exact percentages lets take a look at our poker outs chart:
| After the Flop (2 Cards to Come) | After the Turn (1 Card to Come) | ||||
|---|---|---|---|---|---|
| Outs | Rule of 4 | Exact % | Outs | Rule of 2 | Exact % |
| 1 | 4 % | 4.5 % | 1 | 2 % | 2.3 % |
| 2 | 8 % | 8.8 % | 2 | 4 % | 4.5 % |
| 3 | 12 % | 13.0 % | 3 | 6 % | 6.8 % |
| 4 | 16 % | 17.2 % | 4 | 8 % | 9.1 % |
| 5 | 20 % | 21.2 % | 5 | 10 % | 11.4 % |
| 6 | 24 % | 25.2 % | 6 | 12 % | 13.6 % |
| 7 | 28 % | 29.0 % | 7 | 14 % | 15.9 % |
| 8 | 32 % | 32.7 % | 8 | 16 % | 18.2 % |
| 9 | 36 % | 36.4 % | 9 | 18 % | 20.5 % |
| 10 | 40 % | 39.9 % | 10 | 20 % | 22.7 % |
| 11 | 44 % | 43.3 % | 11 | 22 % | 25.0 % |
| 12 | 48 % | 46.7 % | 12 | 24 % | 27.3 % |
| 13 | 52 % | 49.9 % | 13 | 26 % | 29.5 % |
| 14 | 56 % | 53.0 % | 14 | 28 % | 31.8 % |
| 15 | 60 % | 56.1 % | 15 | 30 % | 34.1 % |
| 16 | 64 % | 59.0 % | 16 | 32 % | 36.4 % |
| 17 | 68 % | 61.8 % | 17 | 34 % | 38.6 % |
As you can see the Rule of 4 and 2 does not give us the exact %, but it is pretty close and a nice quick and easy way to do the math in your head.
Now lets summarise what we have calculated so far:
- We estimate that to win the hand you have 12 Outs
- We have calculated that after the flop with 2 cards still to come there is approximately a 48% chance you will hit one of your outs.
Now we know the Odds of us winning, we need to look at the return we will get for our gamble, or in other words the Pot Odds.
Pot Odds
When we calculate the Pot Odds we are simply looking to see how much money we will win in return for our bet. Again it’s a very simple calculation…
Pot Odds Formula
Pot Odds = Total Pot divided by the Bet I would have to call
What are the pot odds after the flop with our opponent having bet 10c?
- Total Pot = 20c + 10c bet = 30 cents
- Total Bet I would have to make = 10 cents
- Therefore the pot odds are 30 cents divided by 10 cents or 3 to 1.
What does this mean? It means that in order to break even we would need to win once for every 3 times we lose. The amount we would win would be the Total Pot + the bet we make = 30 cents + 10 cents = 40 cents.
| Bet number | Outcome | Stake | Winnings |
|---|---|---|---|
| 1 | LOSE | 10 cents | Nil |
| 2 | LOSE | 10 cents | Nil |
| 3 | LOSE | 10 cents | Nil |
| 4 | WIN | 10 cents | 40 cents |
| TOTAL | BREAKEVEN | 40 cents | 40 cents |
Break Even Percentage
Now that we have worked out the Pot Odds we need to convert this into a Break Even Percentage so that we can use it to make our decision. Again it’s another simple calculation that you can do in your head.
Break Even Percentage
Break Even Percentage = 100% divided by (Pot odds added together)
Let me explain a bit further. Pot Odds added together means replace the “to” with a plus sign eg: 3 to 1 becomes 3+1 = 4. So in the example above our pot odds are 3 to 1 so our Break Even Percentage = 100% divided by 4 = 25%
Note – This only works if you express your pot odds against a factor of 1 eg: “3 to 1” or “5 to 1” etc. It will not work if you express the pot odds as any other factor eg: 3 to 2 etc.
So… Should You call?
So lets bring the two elements together in our example hand and see how we can use the new poker math techniques you have learned to arrive at a decision of whether to continue in the hand or whether to fold.
To do this we compare the percentage probability that we are going to hit one of our Outs and win the hand, with the Break Even Percentage.
Should I Call?
- Call if…… Probability of Hitting an Out is greater than Pot Odds Break Even Percentage
- Fold if…… Probability of Hitting an Out is less than Pot Odds Break Even Percentage
Our calculations above were as follows:
- Probability of Hitting an Out = 48%
- Break Even Percentage = 25%
If our Probability of hitting an out is higher than the Break Even percentage then this represents a good bet – the odds are in our favour. Why? Because what we are saying above is that we are going to get the winning hand 48% of the time, yet in order to break even we only need to hit the winning hand 25% of the time, so over the long run making this bet will be profitable because we will win the hand more times that we need to in order to just break even.
Hand Walk Through #2
Lets look at another hand example to see poker mathematics in action again.
Before the Flop:
- Blinds: 5 cents / 10 cents
- Your Position: Big Blind
- Your Hand: K 10
- Before Flop Action: Everyone folds to the dealer who calls and the small blind calls, you check.
Two people have called and per the Starting hand chart you should just check here, so the Total Pot before the flop = 30 cents.
Flop comes down Q J 6 and the Dealer bets 10c, the small blind folds.
Do we call? Lets go through the thought process:
How has the Flop helped my hand?
It hasn’t but we do have some draws as we have an open ended straight draw (any Ace or 9 will give us a straight) We also have an overcard with the King.
How has the Flop helped my opponent?
The Dealer did not raise before the flop so it is unlikely he is holding a really strong hand. He may have limped in with high cards or suited connectors. At this stage our best guess is to assume that he has hit top pair and holds a pair of Queens. It’s possible that he hit 2 pair with Q J or he holds a small pair like 6’s and now has a set, but we come to the conclusion that this is unlikely.
How many Outs do we have?
So we conclude that we are facing top pair, in which case we need to hit our straight or a King to make top pair to hold the winning hand.
- Open Ended Straight Draw = 8 Outs (4 Aces and 4 Nines)
- King Top Pair = 3 Outs (4 Kings less the King in our hand)
- Total Outs = 11 Probability of Winning = 11 x 4 = 44%
What are the Pot Odds?
Total Pot is now 40 cents and we are asked to call 10 cents so our Pot odds are 4 to 1 and our break even % = 100% divided by 5 = 20%.
Decision
So now we have quickly run the numbers it is clear that this is a good bet for us (44% vs 20%), and we make the call – Total Pot now equals 50 cents.
Turn Card
Turn Card = 3 and our opponent makes a bet of 25 cents.
After the Turn Card
This card has not helped us and it is unlikely that it has helped our opponent, so at this point we still estimate that our opponent is still in the lead with top pair.
Outs
We still need to hit one of our 11 Outs and now with only the River card to come our Probability of Winning has reduced and is now = 11 x 2 = 22%
Pot Odds
The Total Pot is now 75 cents and our Pot odds are 75 divided by 25 = 3 to 1. This makes our Break Even percentage = 100% divided by 4 = 25%
Decision
So now we have the situation where our probability of winning is less than the break even percentage and so at this point we would fold, even though it is a close call.
Summary
Well that was a very heavy lesson, but I hope you can see how Poker Maths doesn’t have to be intimidating, and really they are just some simple calculations that you can do in your head. The numbers never lie, and you can use them to make decisions very easy in Poker.
You’ve learnt some important new skills and it’s time to practise them and get back to the tables with the next stage of the Poker Bankroll Challenge.
Poker Bankroll Challenge: Stage 3
- Stakes: $0.02/$0.04
- Buy In: $3 (75 x BB)
- Starting Bankroll: $34
- Target: $9 (3 x Buy In)
- Finishing Bankroll: $43
- Estimated Sessions: 3
Use this exercise to start to consider your Outs and Pot Odds in your decision making process, and add this tool to the other tools you have already put into practice such as the starting hands chart.
Pot odds is a fundamental and mathematical concept used in poker. Before you understand what pot odds are, take a look at the options below:
Option A: If you risk 1 cookie, you will get 2 cookies.
Option B: If you risk 1 cookie, you will get 5 cookies.
Which option will you choose? Definitely option B. You get 5 cookies for risking 1 cookie!
What if I replace cookie with 1 million dollars? How will it look like?
Option A: If you risk $1 million, you will get $2 million.
Option B: If you risk $1 million, you will get $5 million.
Notice any difference? The values have changed, but the ratio between the reward and risk is still the same. If you have noticed this difference, you have already grasped the meaning of pot odds!
So, without any further ado, let’s delve into the fundamental concept in poker!
What are Pot Odds in Poker?
Poker pot odds are a mathematical expression of risk and reward. Pot odds tell you how much do you need to risk in order to win a reward. It is the ratio between the reward and the risk.
Reward = Pot to be Won
The pot can be at any point of the game – preflop, flop, turn or river.
Risk = How much you need to risk in order to win the pot
The risk is the size of someone’s bet/raise/re-raise you are facing. It is the amount you need to call in order to win the pot.
Pot odds = Reward : Risk
It is the ratio of the size of the pot (reward) to the amount you have to call (risk).
For example:
If there is $6 in the pot and your opponent bets $3, the pot becomes $9. In order to win the pot of $9, you need to call $3. So, what are the odds?
Reward = $9 (Size of the Pot)
Risk = $3 (Size of the Call)
Pot Odds = $9(Reward):$3(Risk)
= 9:3, which can be simplified to 3:1
Hence, the pot odds are 3:1. You can look at these odds in two ways.
- You need to pay 1/3 of the pot for a chance to win the whole pot
- You will get 3X the reward of your risk
Poker Pot Odds Example
Alert! This can be a bit mathematical but an easy hack to learn the odds quickly is available right after the example.
So, have some patience and continue reading…
In this example, we will not be looking at the hole cards so that you are solely focussed on the concept of poker odds.
Here’s the situation: You are on the Button in a $1/$2 6-max game. The Under the Gun (UTG) calls $2. The Middle Position (MP) raises to $5. Let’s calculate the pot odds.
If you don’t know what positions are, go through this: Poker Positions Explained
Preflop
Total pot (Reward) = $1 (small blind) +$2 (big blind) + $2 (UTG’s call) + $5 (MP’s raise)
= $10
Amount to Call (Risk) = $5
Pot Odds = $10 (Reward):$5 (Risk)
= 2:1
You decide to call, and others fold. The total pot is now $15 ($10 in the pot + $5 your call)
Flop
On the flop, the MP makes a half-size pot bet of $7.5. What are the odds now?
Total Pot = $15 (already in the pot) + $7.5 (MP’s bet)
= $22.5
Amount to Call = $7.5
Pot Odds = $22.5:$7.5
= 3:1
Pot Odds Poker Explained Odds
You decide to call, and the total pot is now $30 ($22.5 in the pot +$7.5 your call).
Turn
On the turn, the MP makes a quarter of a pot-size bet of $7.5. What are the odds now?
Total Pot = $30 (already in the pot) + $7.5 (MP’s bet)
= $37.5
Amount to Call = $7.5
Pot Odds = $37.5:$7.5
= 5:1

You decide to call, and the total pot is now $45 ($37.5 in the pot + $7.5 your call).
River
On the river, the MP makes a full pot-size bet of $45. What are the odds now?
Total Pot = $45 (already in the pot) + $45 (MP’s bet)
= $90
Amount to Call = $45
Pot Odds = $90:$45
= 2:1
The pot odds on the river is now 2:1. So, if you call, you will get 2X the reward for your call.
As you can see, the odds increase or decrease on different streets. By using the poker odds, you get a clear picture of the reward you will earn for the risk you take.
A Shortcut to Know Your Pot Odds
An easy way to know the odds is to know how much is in the pot and the percentage of the pot your opponent bets.
- What’s the Pot Size?
- What Percentage of the Pot is Your Opponent Betting?
For example, if the pot is $100 and your opponent bets $25, you can say that he is making a 1/4 pot-size bet or he is betting 25% of the pot.
You can save this chart or print it and paste it on a wall next to your computer.
Why are Pot Odds used in Poker?
Pot odds tell you the ratio between the reward and the risk. It helps you to understand how much you need to risk to win the reward. But the real question is, “Is it worth the risk?” For that, you need to compare your card odds with the pot odds.
What are Card Odds?
It is the ratio of cards in the deck that you don’t want to the cards that you want. In other words, it is the ratio of unwanted cards and outs. If you don’t know what outs are, you can click here: How to Calculate Outs in Poker.
Card Odds = Cards we don’t need : Cards we need
Let’s look at the example below to understand this concept better:
Your Hand: 7♦ 6♦
Flop: 8♦ K♣ 2♦
Your opponent bets $25 into a pot of $100. The total pot is $125. You need to call $25 for a chance to win $125.
So, the pot odds are $125:$25 or 5:1.
In this scenario, you have 9 outs to complete your flush draw. Let’s calculate the odds now.
- A deck has 52 cards.
- We know 5 cards out of those 52 cards – Our 2 Hole Cards and 3 cards on the Flop.
- 52 – 5 = 47. There are 47 cards in the deck that we don’t know.
- There are 9 outs that will help us to make the flush. We need those 9 cards (outs).
- 47 – 9 = 38. We don’t need those 38 cards.
- Card Odds = Cards we don’t need : Cards we need
- Card Odds = 38:9
- 38:9 can be simplified as 4.2:1 or roughly 4:1
The card odds tell us that the odds of hitting a diamond-suited card is 4:1. This means that there is a possibility that a diamond-suited card is in the deck once every 4 cards. In other words, for every 4 times, you won’t hit a diamond, 1 time you will.
Compare Pot Odds with Card Outs
The golden rule is that thepot odds should be greater than the card outs. When the odds from the pot are bigger than the odds of hitting an out, you will be winning more money than losing in the long run. So, the reward should be bigger than the risk.
Pot Odds > Card Outs
In the above example, we have the following odds:
Pot Odds = 5:1
Card Odds = 4:1
Pot Odds > Card Outs
We should call here as the pot odds are greater than card odds.
Card Odds Chart
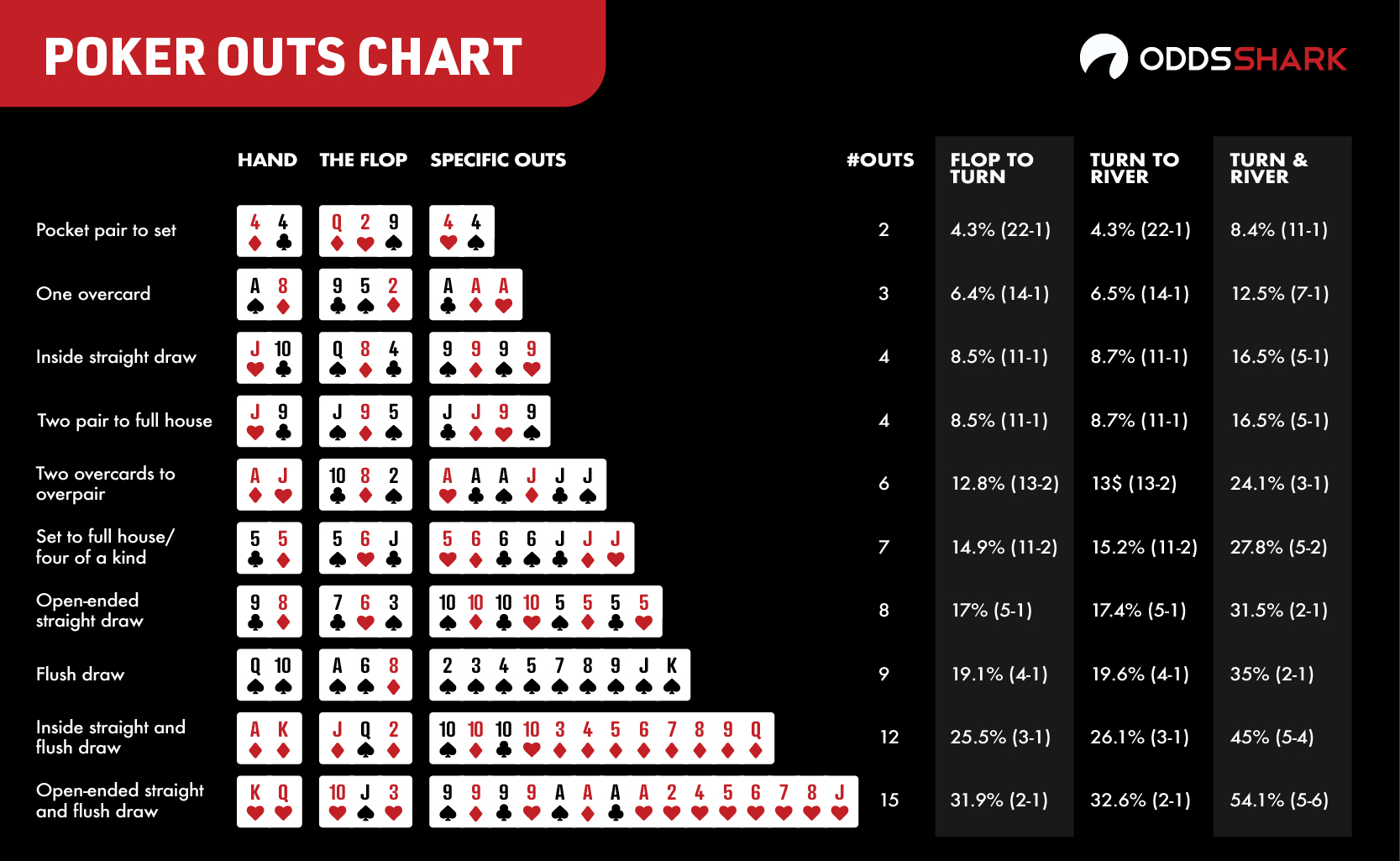
It may be very difficult to do the addition and division to find the card odds while playing poker. You can save this card odds chart or print it to paste it on the wall. The chart has the common draw scenarios with the poker outs that you might face while playing poker. With a bit of practice, you will remember the important card odds.
* The last column All-in on the Flop (2 Cards to Come) is in a situation when you or your opponent go all-in on the flop. In an all-in situation, you don’t have to call bets on the turn or river. So, you will see 2 cards till the river. Seeing 2 cards instead of 1 improves your odds.
Let’s look at the example below for a quick exercise.
Your Hand: 7♦ 6♦
Turn: 8♦ K♣ 2♦ J♠
You have a flush draw with 9 outs.
Bet Size #1
Your opponent makes a quarter of a pot-size bet of $25 into a pot of $100. The total pot is now $125. You need to call $25 for a chance to win $125.
Pot Odds: 5:1 ($125:$25)
Card Odds: 4.1:1 (Look at the chart)
Pot Odds > Card Odds
Here, you can call as the pot odds are greater than the card odds. This means that you will be winning more money than losing in the long run.
Bet Size #2
In the same example, if your opponent makes a full pot-size bet of $100 into a pot of $100, the total pot becomes $200. You need to call $100 for a chance to win $200.
Pot Odds: 2:1 ($200:$100)
Card Odds: 4.1:1 (Look at the chart)
Card Odds > Pot Odds
Here, the card odds are greater than the pot odds. Although you might hit a flush on the river, calling here won’t be profitable in the long run. So, it will be wise to fold here.
Calculating Pot Odds Using the Percentage Method
Another way of calculating odds in poker is by using the percentage method. There are three simple steps in calculating the odds using the percentage method.
Step 1: Calculate the Final Pot
This is the major difference between the ratio method and the percentage method. In the percentage method, you need to add your call amount to the total pot to calculate the final pot. For example, if there is $6 in the pot and your opponent bets $3, the total pot becomes $9. Now add your call amount, which is $3, to calculate the final pot.
Total Pot = $6 (Already in the pot) + $3 (Opponent’s Bet)
= $9
Final Pot = $9 (Total Pot) + $3 (Call Amount)
= $12
Step 2: Divide the Call Amount by the Final Pot
Call Amount = $3
Final Pot = $12
3/12 = 0.25
Step 3: Multiply by 100
Multiply by 100 to get the percentage.
0.25 X 100 = 25%
So, the pot odds are 25%.
Poker Pot Odds Example Using the Percentage Method
Alert! This can be a bit mathematical but an easy hack to learn the odds quickly is available right after the example.
So, have some patience and continue reading…
Let’s review the example without looking at the hole cards to find the odds percentage.
You are on the Button in a $1/$2 6-max game. The Under the Gun (UTG) calls $2. The Middle Position (MP) raises to $5. Let’s calculate the odds.
Preflop
Total pot = $1 (small blind) +$2 (big blind) + $2 (UTG’s call) + $5 (MP’s raise)
= $10
Amount to Call = $5
Final Pot = $10 (Total Pot) + $5 (Call Amount)
= $15
Pot Odds = $5 (Call Amount) / $15 (Final Pot)
= 0.33
0.33 X 100 = 33%
So, the pot odds are 33%.
You decide to call, and others fold. The total pot is now $15 ($10 in the pot + $5 your call)
Flop
On the flop, the MP makes a half-size pot bet of $7.5. What are the odds now?
Total Pot = $15 (already in the pot) + $7.5 (MP’s bet)
= $22.5
Amount to Call = $7.5
Final Pot = $22.5 (Total Pot) + $7.5 (Call Amount)
= $30
Pot Odds = $7.5 (Call Amount) / $30 (Final Pot)
= 0.25
0.25 X 100 = 25%
So, the pot odds are 25%.
You decide to call, and the total pot is now $30 ($22.5 in the pot +$7.5 your call).
Turn
On the turn, the MP makes a quarter of a pot-size bet of $7.5. What are the odds now?
Total Pot = $30 (already in the pot) + $7.5 (MP’s bet)
= $37.5
Amount to Call = $7.5
Final Pot = $37.5 (Total Pot) + $7.5 (Call Amount)
= $45
Pot Odds = $7.5 (Call Amount) / $45 (Final Pot)
= 0.17
0.17 X 100 = 17%
So, the pot odds are 17%.
You decide to call, and the total pot is now $45 ($37.5 in the pot + $7.5 your call).
River
On the river, the MP makes a full pot-size bet of $45. What are the odds now?
Total Pot = $45 (already in the pot) + $45 (MP’s bet)
= $90
Amount to Call = $45
Final Pot = $90 (Total Pot) + $45 (Call Amount)
= $135
Pot Odds = $45 (Call Amount) / $135 (Final Pot) = 0.33
0.33 X 100 = 33%
So, the pot odds are 33%.
A Shortcut to Know Your Pot Odds Percentage
An easy way to know the odds is to know how much is in the pot and the percentage of the pot your opponent bets.
- What’s the Pot Size?
- What Percentage of the Pot is Your Opponent Betting?
For example, if the pot is $100 and your opponent bets $25, you can say that he is making a 1/4 pot-size bet or he is betting 25% of the pot.
You can save this pot odds chart or print it and paste it on a wall next to your computer.
Pot Odds Poker Explained Payouts
How is the Percentage used in Poker?
In the percentage method, you need to find the card equity and compare it with odds percentage to make a decision. Card equity is as same as card odds. Instead of using a ratio, it is expressed in percentage.
How to Find Card Equity?
Card equity can be accurate if you know what range of hands your opponents are holding. There are many equity calculators available online. Since this is an introductory chapter on poker pot odds, we will teach you the simplest way to calculate card equity.
On the Flop Waiting for the Turn – Number of Outs X 4
On the Turn Waiting for the River – Number of Outs X 2
Let’s look at the example below to calculate the equity.
Your Hand: 7♦ 6♦
Flop: 8♦ K♣ 9♠
You have an open-ended straight draw with 8 outs.
Equity = 8 outs x 4
= 32%
Turn: 8♦ K♣ 9♠ 2♥
Equity = 8 x 2
= 16%
Compare Pot Odds with Equity
The golden rule is that theequity should be greater than the pot odds. When the equity is greater than the pot odds, you will be winning more money than losing in the long run. Here, the reward is bigger than the risk.
Equity > Pot Odds
Let’s look at the example below to compare the odds and equity.
Your Hand: 7♦ 6♦
Turn: 8♦ K♣ 2♦ J♠
You have a flush draw with 9 outs.
Bet Size #1
Your opponent makes a quarter of a pot-size bet of $25 into a pot of $100. The total pot is now $125. The final pot is $150 (total pot + call amount).
Pot Odds: 17% (25/150 X 100)
Equity: 9 (outs) X 2 (Turn)
= 18%
Equity > Pot Odds
Here, you can call as the equity is greater than the pot odds. This means that you will be winning more money than losing in the long run.
Bet Size #2
In the same example, if your opponent makes a full pot-size bet of $100 into a pot of $100, the total pot becomes $200. The final pot is $300 (total pot + call amount).
Pot Odds: 33% (100/300 X 100)
Equity: 9 (outs) X 2 (Turn)
= 18%
Pot Odds > Equity
Here, the pot odds are greater than the equity. Although you might hit a flush on the river, calling here won’t be profitable in the long run. So, it will be wise to fold here.
An easy way to find out how much equity is required for you to call is to find out the percentage of the pot your opponent bets. Remember these odds against your opponent’s bet sizes.
Conclusion
It might be a little overwhelming for the first time to grasp the concept of pot odds. However, with a bit of practice, you will get used to it. We recommend you to save all the charts or print them and paste it on the wall to take quick decisions. Poker is a mathematical game, and if you get your numbers right, you will always win money in the long run!